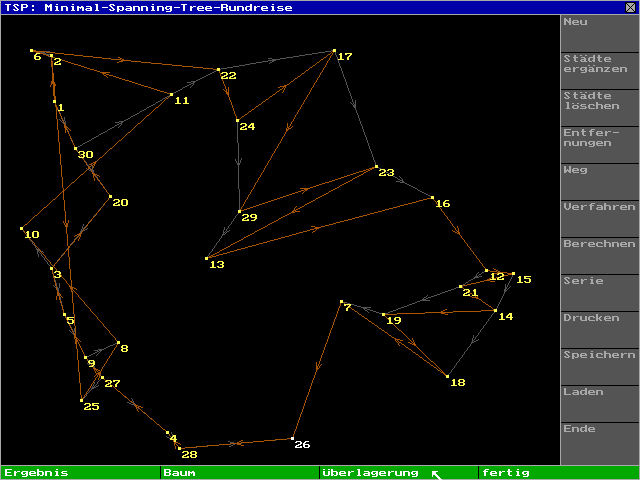
Abbildung 4.2: Überlagerung von MST und Rundreise
Heuristiken erzeugen Näherungslösungen des Traveling Salesman
Problems. Abschnitt 4.1 stellt bekannte Verfahren vor,
Abschnitt 4.2 enthält eigene Entwicklungen.
Wie im letzten Kapitel zu sehen war, ist die Untersuchung aller möglichen Touren schon bei relativ kleinen Städtezahlen nicht mehr praktikabel, so daß man auf andere Verfahren angewiesen ist. Ein Ansatz sind die sogenannten Heuristiken. Sie garantieren nicht, die optimale Lösung zu finden, liefern dafür aber mit akzeptablem Rechenaufwand mehr oder weniger gute Ergebnisse. In diesem Kapitel werden konstruktive Heuristiken behandelt, die neue Rundreisen konstruieren. Im Gegensatz dazu verbessern optimierende Heuristiken (Kap. 5) schon bestehende Touren.
...
Bei Algorithmen, deren Ergebnis von der Auswahl eines Startpunktes abhängt, wurden die Berechnungen für alle Startpunkte durchgeführt und die beste Tour ausgewählt (automatische Startpunktwahl, s. 4.1.2).
...

Abbildung 4.2: Überlagerung von MST und Rundreise
Bei den bisherigen Verfahren war es nicht möglich, eine Aussage über die
Qualität der gelieferten Tour im Vergleich zur optimalen Lösung zu machen.
Dies ist beim Minimal-Spanning-Tree-Rundreise-Algorithmus zumindest im
metrischen Fall anders. Wie der Name schon andeutet, geht er vom Minimal
Spanning Tree des Graphen aus: Verdoppelt man alle Kanten des MST, so erhält
man eine Rundreise, die allerdings jede Stadt mindestens zweimal enthält. Um
daraus eine Tour zu machen, kürzt man ab, d. h. man durchläuft den Rundweg von
einer Anfangsstadt ausgehend, und jedes Mal, wenn man einen Ort zum zweitenmal
besuchen würde, überspringt man ihn und geht direkt zum nächsten weiter.
Wie schon in Abschnitt 3.2 erläutert, stellt die Länge des MST eine untere Schranke für die Längen der Touren des zugehörigen TSP dar. Andererseits verringert sich, falls die Dreiecksungleichung gilt, die Länge der aus dem verdoppelten Minimal Spanning Tree entstandenen Rundreise durch das Abkürzen bzw. sie bleibt maximal gleich, d. h. die Länge des Endergebnisses beträgt höchstens das zweifache der Kosten des MST. Daraus folgt:
Länge der Tour / Länge der optimalen Tour <= 2
Das Minimal-Spanning-Tree-Rundreise-Verfahren liefert im metrischen Fall also eine Tour, die maximal doppelt so lang wie die optimalen Tour ist. Im nichtmetrischen Fall ist dies hingegen nicht gewährleistet, da sich ohne die Dreiecksungleichung beim 'Abkürzen' die Rundreise auch verlängern kann.Für die Erzeugung des Minimal Spanning Tree wird eine modifizierte Version der PRIM-Prozedur aus Programm 3.2 verwendet. PRIM_R verzichtet auf die Optimierung, durch die bei zwei aufeinanderfolgenden Kanten, bei denen der Endknoten der ersten mit dem Startknoten der zweiten übereinstimmt, die trennende Null und die doppelte Stadtnummer weggelassen wird. Der Eintrag einer Kante besteht also immer aus drei Zeichen, nämlich aus einer Null zur Trennung, dem Startort und der Nummer des Endortes, was die Berechnung der Rundreise in der Prozedur MSTR vereinfacht. Dort wird die Tour in der Variablen W vom Typ WEG aufgebaut, indem sie mit ANFANG initialisiert und durch wiederholten Aufruf von NAECHSTE erweitert wird, bis die Stringlänge der Stadtanzahl entspricht.
NAECHSTE übernimmt die zentrale Aufgabe des Algorithmus, ausgehend von der übergegebenen vorherigen Stadt N die nächste aus dem verdoppelten MST zu ermitteln und, falls notwendig, dabei Orte zu überspringen, also abzukürzen. Die Verdopplung der Kanten wird dabei nicht tatsächlich durchgeführt, sondern statt dessen jede in Hin- und Rückrichtung betrachtet: In den Zeilen 51-55 wird nach einer Kante gesucht, die N entweder als Start- oder als Endpunkt enthält und der jeweils andere Punkt als neues N verwendet. Dies wird solange wiederholt, bis man zu einem N kommt, das noch nicht in W enthalten ist. Aufgrund der Reihenfolge der Bearbeitung ist gewährleistet, daß im nächsten Durchlauf nicht die gleiche Kante in umgekehrter Richtung betrachtet wird, was eine Endlosschleife zur Folge hätte. Hat man schließlich einen noch nicht in W enthaltenen Wert gefunden, so wird dieser als nächste anzufügende Stadt an MSTR zurückgegeben.
1: program p_mstr; (* Minimal-Spanning-Tree-Rundreise, Thomas Klein 1999 *)
2: uses graph,grafik,maus,tsp;
3: var anfang:stadtnr;
4: mst:weg;
5: wahl:byte;
6: desc:menu_desc;
7:
8: procedure prim_r(var t:weg);
9: (* berechnet min. erzeugenden Baum, Ergebnis im
10: Format '0 start1 ende1 0 start2 ende2 0 ...' *)
11: var i,j:stadtnr;
12: e:array [1..maxstadtquad] of record i,j:stadtnr; end;
13: w:array [1..maxstadt] of entfernung;
14: s:set of stadtnr;
15: l:entfernung;
16: k:word;
17: begin
18: k:=0;
19: for i:=1 to stadtanzahl do
20: for j:=1 to stadtanzahl do begin
21: inc(k); e[k].i:=i; e[k].j:=j
22: end;
23: w[1]:=0; s:=[1..stadtanzahl]; t:='';
24: for i:=2 to stadtanzahl do w[i]:=maxentfernung;
25: while s<>[] do begin
26: l:=maxentfernung;
27: for j:=1 to stadtanzahl do
28: if (j in s) and (w[j]<=l) then begin i:=j; l:=w[j]; end;
29: s:=s-[i];
30: if e[i].i<>e[i].j then t:=t+chr(0)+chr(e[i].i)+chr(e[i].j);
31: for k:=1 to stadtanzahl*stadtanzahl do begin
32: i:=e[k].i; j:=e[k].j;
33: if not(i in s) and (j in s) then begin
34: l:=entftab[i,j];
35: if w[j]>l then begin w[j]:=l; e[j]:=e[k]; end;
36: end;
37: end;
38: end;
39: end;
40:
41: procedure mstr(mst:weg;anfang:stadtnr;var w:weg);
42: (* berechnet ausgehend von Startpunkt anfang aus
43: min. erzeugenden Baum mst eine TSP-Lösung *)
44: var n:stadtnr;
45: function naechste(n:stadtnr):stadtnr;
46: var p:integer;
47: n1,n2:stadtnr;
48: begin
49: p:=-2;
50: while pos(chr(n),w)<>0 do begin
51: repeat
52: inc(p,3); if p>length(mst) then p:=1;
53: n1:=ord(mst[p+1]); n2:=ord(mst[p+2]);
54: until (n1=n) or (n2=n);
55: if n1=n then n:=ord(mst[p+2]) else n:=ord(mst[p+1]);
56: end;
57: naechste:=n;
58: end;
59: begin
60: w:=chr(anfang); n:=anfang;
61: while length(w)<>stadtanzahl do begin
62: n:=naechste(n); w:=w+chr(n);
63: end;
64: w:=w+chr(anfang);
65: end;
66:
67: begin
68: if tspinit('TSP: Minimal-Spanning-Tree-Rundreise','Berechnen') then
69: while tspmenue([0..255]) do begin
70: meldung('Startpunkt wählen!',green,white);
71: anfang:=stadtwahl(255);
72: start; prim_r(mst); mstr(mst,anfang,aktuell); stop;
73: wahl:=1; menue(-4,'Ergebnis|Baum|Überlagerung|fertig',green,white,black,desc);
74: repeat
75: case wahl of
76: 1: zeichne_weg(aktuell,true,brown);
77: 2: zeichne_weg(mst,true,darkgray);
78: 3: begin
79: zeichne_weg(mst,true,darkgray);
80: zeichne_weg(aktuell,false,brown);
81: end;
82: end;
83: zeichne_karte(false,yellow);
84: warte_maus(0); zeige_maus; warte_maus(1); verstecke_maus;
85: wahl:=chkmenu(mausx,mausy,desc);
86: until wahl=4;
87: wegkarte(aktuell,true,brown,yellow);
88: laenge_aus(aktuell); zeit_aus(true);
89: end;
90: closegraph;
91: end.
Das Programm erlaubt es, neben der berechneten Rundreise auch den Ausgangs-MST sowie eine Überlagerung beider anzuzeigen, Abbildung 4.2 zeigt dies mit dem gleichen erzeugenden Baum wie in Abschnitt 3.2.
Das Problem des Nearest-Neighbour-Algorithmus ist, daß durch die lokale Betrachtungsweise nur der jeweils nächsten einzubindenden Stadt ohne Berücksichtigung des Gesamtaufbaus der Tour die letzten Kanten und insbesondere die Rückkehr zum Anfangspunkt sehr lang werden können. Das Start-Nachbar(SN)-Verfahren versucht dies dadurch zu vermindern, daß nicht nur die Entfernungen zum folgenden Ort klein, sondern auch der Abstand zum ersten Ort möglichst groß sein soll, was bewirkt, daß der Weg zuerst vom Start 'weggetrieben' wird und am Ende Punkte in der Nähe der Startstadt übrigbleiben. Realisiert wird dies, indem als nächster Ort derjenige ausgewählt wird, für den der Quotient (4.3)
ENTFTAB[aktueller Ort,nächster Ort] / ENTFTAB[nächster Ort,Anfang]
minimal ist.
1: program p_sn; (* Start-Nachbar-Verfahren, Thomas Klein 1999 *)
2: uses graph,tsp;
3: var anfang:stadtnr;
4:
5: procedure sn(anfang:stadtnr;var w:weg);
6: (* Start-Nachbar mit Startpunkt anfang,
7: nächster Punkt i: Abstand(aktuell,i)/Abstand(i,anfang) min. *)
8: var n,i,j:stadtnr;
9: m,l:real;
10: begin
11: n:=anfang; w:=chr(n);
12: while length(w) < stadtanzahl do begin
13: m:=maxentfernung;
14: for i:=1 to stadtanzahl do
15: if pos(chr(i),w)=0 then begin
16: l:=entftab[n,i]/entftab[i,anfang];
17: if l < m then begin j:=i; m:=l; end;
18: end;
19: n:=j; w:=w+chr(n);
20: end;
21: w:=w+chr(anfang);
22: end;
23:
24: begin
25: if tspinit('TSP: Start-Nachbar-Verfahren','Berechnen') then
26: while tspmenue([0..255]) do begin
27: meldung('Startpunkt wählen!',green,white);
28: anfang:=stadtwahl(255);
29: start; sn(anfang,aktuell); stop;
30: wegkarte(aktuell,true,brown,yellow);
31: laenge_aus(aktuell); zeit_aus(true);
32: end;
33: closegraph;
34: end.
Im Falle einer symmetrischen Entfernungsmatrix gibt es beim Start-Nachbar-Verfahren noch ein Problem: Bei der Bestimmung der ersten Kante ist der aktuelle Ort gleich dem Anfangspunkt, so daß der Quotient (4.3) für alle Städte gleich eins ist. Daher wird in Programm 4.10 in diesem Fall immer die in der Reihenfolge erste ausgewählt. Das Optimierte Start-Nachbar(OSN)-Verfahren geht deshalb im ersten Schritt wie beim Nearest-Neighbour-Algorithmus zum nächstgelegenen Ort und benutzt erst danach die Start-Nachbar-Vorgehensweise:
1: program p_osn; (* optimiertes Start-Nachbar-Verfahren, Thomas Klein 1999 *)
2: uses graph,tsp;
3: var anfang:stadtnr;
4:
5: procedure osn(anfang:stadtnr;var w:weg);
6: (* zuerst von anfang zum naechsten Punkt, dann Start-Nachbar *)
7: var n,i,j:stadtnr;
8: m,l:real;
9: begin
10: n:=anfang; w:=chr(n);
11: while length(w) < stadtanzahl do begin
12: m:=maxentfernung;
13: for i:=1 to stadtanzahl do
14: if pos(chr(i),w)=0 then begin
15: if length(w)=1 then
16: l:=entftab[n,i]
17: else
18: l:=entftab[n,i]/entftab[i,anfang];
19: if l < m then begin j:=i; m:=l; end;
20: end;
21: n:=j; w:=w+chr(n);
22: end;
23: w:=w+chr(anfang);
24: end;
25:
26: begin
27: if tspinit('TSP: Optimiertes Start-Nachbar-Verfahren','Berechnen') then
28: while tspmenue([0..255]) do begin
29: meldung('Startpunkt wählen!',green,white);
30: anfang:=stadtwahl(255);
31: start; osn(anfang,aktuell); stop;
32: wegkarte(aktuell,true,brown,yellow);
33: laenge_aus(aktuell); zeit_aus(true);
34: end;
35: closegraph;
36: end.
Wie Tabelle 4.11 zeigt, liefert der Algorithmus im metrischen Fall erkennbar bessere Ergebnisse als Nearest Neighbour. Sie erreichen sogar fast das Niveau von Farthest Insertion, allerdings aufgrund der fehlenden Insertion-Berechnungen mit einem deutlich geringeren Rechenaufwand.
So wie das Nearest-Insertion-Verfahren den nächsten einzufügenden Ort genauso wie der Nearest-Neighbour-Algorithmus auswählt, dann aber das Insertion-Prinzip anwendet, so kann man auch aus dem Start-Nachbar-Verfahren eine Insertion-Variante (Minimum-SN-Insertion) ableiten.
...
Das entsprechende Gegenstück zu Farthest Insertion, Maximum-SN-Insertion, erhält man durch Änderung der Zeilen 12 und 18 in
12: mm:=-maxentfernung; 18: if l > mm then begin mm:=l; n:=j; end;
und Anpassung des Hauptprogramms.
Minimum-OSN-Insertion ist die analog zum OSN-Verfahren an symmetrische Entfernungsmatrizen angepaßte Version von Minimum-SN-Insertion. Die Ergebnisse der hier abgedruckten 'Maximum-Variante' erreichen im metrischen Fall fast die von Farthest Insertion.
...
Bei den bisherigen Start-Nachbar-Insertion-Variationen wurde bei der Auswahl der nächsten einzufügenden Stadt jeweils eine der Größen 'Entfernung zum vorherigen Punkt' und 'Abstand zum Startpunkt' auf Maximalität und die andere auf Minimalität hin optimiert. Ersetzt man den Quotienten (4.3) jedoch durch eine Summe, so gilt für beide die gleiche Richtung. Das Ergebnis sind die Verfahren Minimum-Sum-Insertion, bei dem der Ort ausgewählt wird, für den die Summe minimal ist, und Maximum-Sum-Insertion für den entgegengesetzten Fall.
...
Im metrischen Fall liefert wieder die Maximum-Variante die besseren Ergebnisse, die diesmal sogar diejenigen von Farthest Insertion geringfügig übertreffen:
Minimum-Product-Insertion und Maximum-Product-Insertion verfolgen die gleiche Idee wie Minimum/Maximum-Sum-Insertion, wobei hier statt der Summe das Produkt
ENTFTAB[aktueller Ort,nächster Ort] * ENTFTAB[nächster Ort,Anfang]
verwendet wird. Im Programm 4.14 ist dazu in Zeile 17 das '+' durch '*' zu ersetzen. Maximum-Product-Insertion liefert im metrischen Fall die besten Resultate aller vorgestellten Verfahren.
Während bei den bisherigen Algorithmen meist der metrische Fall im Mittelpunkt stand, sind die Kürzeste-Wege-Rundreise(KWR)-Verfahren speziell für nichtmetrische Entfernungsmatrizen ausgelegt. Wie der Name schon sagt, benutzen sie die Bestimmung von kürzesten Wegen als Basis, und falls die Dreiecksungleichung gilt, ist die direkte Verbindung immer der kürzeste Weg. Gemeinsam ist allen Algorithmen die folgende Vorgehensweise (der Rundweg wird in W aufgebaut):
1: W:=Startort;
2: solange W nicht alle Städte enthält
3: berechne kürzeste Wege vom letzten Ort in W zu allen noch nicht in W
enthaltenen Orten;
4: wähle einen dieser Wege aus und füge ihn an W an;
5: ende{solange}
6: W:=W+Startort;
Der Unterschied zwischen den verschiedenen Varianten liegt darin, wie in
Schritt 4 der anzufügende Weg ausgewählt wird.
Für die Ermittlung der kürzesten Wege wird eine modifizierte Version der DIJKSTRA-Prozedur aus Programm 3.1 verwendet, die kürzeste Wege vom Endpunkt eines übergebenen Weges ohne die sonstigen darin enthaltenen Städte berechnet. Dazu wird in den Zeilen 14-22 von DIJKSTRA_W ein INDEX-Feld aufgebaut, das die Nummern der noch nicht besuchten Orte enthält und über das im eigentlichen Dijkstra-Algorithmus z. B. auf die Entfernungstabelle und die Längen zugegriffen wird.
Beim ersten KWR-Algorithmus wird versucht, mit jedem hinzuzufügenden Weg möglichst viele Städte zu erfassen, d. h. es wird derjenige Weg ausgewählt, der die meisten Orte enthält. Im metrischen Fall besteht jeder natürlich nur aus einer Stadt, so daß alle gleichberechtigt sind und quasi zufällig, nämlich anhand der Reihenfolge, in der sie von DIJKSTRA_W übergeben werden, einer bestimmt wird. Entsprechend schlecht sind in diesem Fall die Resultate.
1: program p_kwr1; (* Kürzeste-Wege-Rundreise 1, Thomas Klein 1999 *)
2: uses graph,grafik,tsp;
3: var anfang:stadtnr;
4: laenge:array [1..maxstadt] of entfernung;
5: wege:array [1..maxstadt] of string[maxstadt];
6:
7: procedure dijkstra_w(w:weg);
8: (* berechnet kuerzeste Wege ohne in w enthaltene Punkte,
9: Startpunkt: Endpunkt v. w, Ergebnis in laenge, wege *)
10: var anfang,n,i,j,k,k0,anzahl_vorlaeufig:stadtnr;
11: index,vorlaeufig,vorgaenger:array [1..maxstadt] of stadtnr;
12: min,pfadlaenge:entfernung;
13: begin
14: (* Index auf nicht in w enthaltene Staedte erstellen *)
15: i:=ord(w[length(w)]); dec(w[0]); n:=0;
16: for j:=1 to stadtanzahl do
17: if pos(chr(j),w)=0 then begin
18: inc(n); index[n]:=j;
19: if j=i then anfang:=n;
20: end else begin
21: wege[j]:=''; laenge[j]:=maxentfernung;
22: end;
23: (* Dijkstra-Algorithmus *)
24: for j:=1 to n do begin
25: vorlaeufig[j]:=j; vorgaenger[j]:=anfang;
26: laenge[index[j]]:=entftab[index[anfang],index[j]];
27: wege[index[j]]:=chr(index[anfang])+chr(index[j]);
28: end;
29: vorlaeufig[anfang]:=n; anzahl_vorlaeufig:=n-1;
30: for i:=1 to n-1 do begin
31: min:=maxentfernung;
32: for k:=1 to anzahl_vorlaeufig do begin
33: j:=vorlaeufig[k];
34: pfadlaenge:=laenge[index[anfang]]+entftab[index[anfang],index[j]];
35: if pfadlaenge < laenge[index[j]] then begin
36: vorgaenger[j]:=anfang;
37: laenge[index[j]]:=pfadlaenge;
38: wege[index[j]]:=wege[index[anfang]]+chr(index[j]);
39: end;
40: if laenge[index[j]] < min then begin
41: min:=laenge[index[j]]; k0:=k;
42: end;
43: end;
44: anfang:=vorlaeufig[k0]; vorlaeufig[k0]:=vorlaeufig[anzahl_vorlaeufig];
45: dec(anzahl_vorlaeufig);
46: end;
47: end;
48:
49: procedure kwr1(var w:weg);
50: (* Kürzeste-Wege-Rundreise, Staedtezahl max. *)
51: var anfang,i,mweg,m,l:stadtnr;
52: begin
53: anfang:=ord(w[length(w)]);
54: while length(w) < stadtanzahl do begin
55: dijkstra_w(w);
56: m:=0;
57: for i:=1 to stadtanzahl do
58: if (wege[i]<>'') and (i<>ord(w[length(w)])) then begin
59: l:=length(wege[i]);
60: if l > m then begin m:=l; mweg:=i; end;
61: end;
62: dec(w[0]); w:=w+wege[mweg];
63: end;
64: w:=w+chr(anfang);
65: end;
66:
67: begin
68: if tspinit('TSP: Kürzeste-Wege-Rundreise 1(max. Städtezahl)',
69: 'Berechnen') then
70: while tspmenue([0..255]) do begin
71: meldung('Startpunkt wählen!',green,white);
72: anfang:=stadtwahl(255); aktuell:=chr(anfang);
73: start; kwr1(aktuell); stop;
74: wegkarte(aktuell,true,brown,yellow);
75: laenge_aus(aktuell); zeit_aus(true);
76: end;
77: closegraph;
78: end.
Hier wird der mittlere Abstand zwischen den Städten der kürzesten Wege, also
Weglänge / Anzahl der Städte auf diesem Weg ,
der möglichst gering sein soll, als Entscheidungskriterium verwendet. Im metrischen Fall ergibt sich daraus das Nearest-Neighbour-Verfahren....
Die dritte Variante versucht, mit den Endpunkten der kürzesten Wege möglichst nahe am Startpunkt zu bleiben, d. h.
ENTFTAB[letzter Ort des Weges,Startort]
soll minimal sein, während KWR 4 in der Tradition von Farthest Insertion und dem Start-Nachbar-Verfahren das Gegenteil anstrebt und den Weg auswählt, für den der Abstand vom Wegende zum Startort maximal ist und damit die besseren Ergebnisse erzielt....
Kürzeste-Wege-Rundreise 5 verbindet KWR 1 und KWR 4, indem sowohl die Anzahl der Städte des jeweiligen Weges als auch der Abstand des Endpunktes zum Startort möglichst groß sein sollen. Als Auswahlkriterium wird daher das Produkt
(Anzahl der Städte auf dem Weg) * ENTFTAB[letzter Ort des Weges,Startort]
dieser beiden Größen verwendet und damit tatsächlich die Resultate von KWR 1-4 für die nichtmetrischen Fälle übertroffen....
Die letzte Variante ist schließlich eine Kombination von KWR 2 und KWR 4, bei der der Abstand vom Wegendpunkt zum Tourstartpunkt maximal, der mittlere Abstand der Städte im Weg jedoch minimal sein soll. Es wird daher der Weg gesucht, für den der Quotient
ENTFTAB[letzter Ort des Weges,Startort] / mittlerer Stadtabstand
maximal ist. Für die nichtmetrischen Fälle erhält man ähnliche Ergebnisse wie bei KWR 5, im metrischen Fall ist der Algorithmus identisch zum Start-Nachbar-Verfahren....
...
Fazit: Kommt es nur auf bestmögliche Resultate an, so liefern Farthest Insertion, Maximum-Sum-Insertion, Minimum-Product-Insertion und Maximum-Product-Insertion für metrische Probleme die besten Ergebnisse. Muß auch die Rechenzeit beachtet werden, so empfiehlt sich die Verwendung des Optimierten Start-Nachbar-Verfahrens. Im nichtmetrischen Fall sind die Ergebnisse von KWR 5 und 6 sowie des Nearest-Neighbour-Algorithmus am besten, wegen seiner Einfachheit ist dabei letzterer im allgemeinen vorzuziehen.